[1주차 공부 키워드] 개념 정리

Posted Mar 27, 2025

By sihyun 14 min read

주차별로 공부 키워드가 주어지는데, 그 키워드를 잘 잡고 가지 않았던것 같아 3주차를 시작하기 전에 이 키워드들을 한번씩 회고해보며, 제 글로 설명해보면 좋을 것 같아서 글을 작성하게 되었습니다.

글의 목차

간단하게 아래 목차별로 개념을 훑어보기

배열
문자열
반복문과 재귀함수
복잡도(BigO, 시간, 공간)
정렬

배열

배열은 많은 데이터를 저장하며, 인덱스를 사용해 그 데이터에 접근할 수 있다.
인덱스 덕분에 빠른 조회가 가능하다는 장점이 있다.

파이썬은 java언어와 다르게 다른 종류의 데이터도 저장할 수 있다.

  
# 문자열, 숫자 같이 저장될 수 있음
arr = ["jungle", 1, 2]

시간 복잡도
- 조회 : O(1)
- 삭제 or 삽입 : 최악인 상황이면 O(n)

문자열

문자열은 "큰 따옴표, '작은 따옴표 안에 작성해주면 된다.

  
a = "jungle is life"

인덱싱이 가능하며 문자열 연산도 가능하다.
(문자열의 각 문자는 인덱스를 통해 접근 가능)

  
a = "jungle"
find_a = a[0] # j
select_a = a[2:4] # ng

b = "is life"
combined_a = a + " " + b
print(combined_a) # jungle is life

그다음으로는 문자열에서 많이 사용했던 메서드이다.

strip() : 양쪽 공백 제거
- 스페이스, 탭, 개행문자(\n)제거
split() : 문자열 나누기
.join(리스트) : 문자열 합쳐서 반환
- ‘구분자’.join(리스트) : 구분자를 넣어 문자열 합쳐서 반환

반복문과 재귀함수

반복문은 특정 조건이 참(True)인 경우 계속 반복하며, 거짓(False)이 되면 멈춘다.

재귀함수는 자기 자신을 다시 호출하는 함수다.
또한 함수를 반복적으로 호출하기에 스택 메모리를 사용한다.
(*) 주의점 : 종료조건을 꼭 필수적으로 작성해주어야한다! (무한 재귀가 발생할 수 있기 때문에)

반복문으로 작성한 코드는 재귀함수로도 작성가능하며, 재귀함수로 작성한 코드는 반복문으로 작성이 가능하다.

반복문으로 구현한 팩토리얼

  
import sys

def factorial(n):
  result = 1

  for i in range(1, n + 1):
    result *= i
  return result

N = int(sys.stdin.readline())
print(factorial(N))

재귀함수로 구현한 팩토리얼

  
import sys

def factorial(n):
  if (n > 0):
    return n * factorial(n-1)
  elif (n == 0):
    return 1


N = int(sys.stdin.readline())
print(factorial(N))

반복문과 재귀함수의 차이점

반복문은 스택 메모리를 사용하지 않아 메모리 사용량이 적고 빠른 실행속도를 가지고 있다.
재귀함수는 함수 호출마다 스택 프레임이 쌓여 무한 재귀라면 스택 오버플로우를 일으킬 수 있다.

단순한 반복 작업에선 반복문이 유리하고,
문제의 구조가 재귀인 경우 반복문 보다 재귀함수를 쓰는게 논리적으로 간결하고 이해하기 쉽다.

복잡도(BigO, 시간, 공간)

복잡도는 알고리즘의 성능을 나타내는 척도다.
복잡도를 표현할때 BigO(빅오)표기법을 사용한다.

알고리즘 문제를 풀때면 같은 문제여도 어떤 방식으로 풀었냐에 따라 걸리는 시간과 실패하거나 성공하는 경우가 있다. 이때 복잡도를 통해, 내 코드가 효율적인 코드인지 판단할 수 있다.

복잡도는 시간, 공간복잡도로 나눌 수 있다.

시간 복잡도 : 알고리즘을 위해 필요한 연산의 횟수
- 얼마나 오래 걸리는지
공간 복잡도 : 알고리즘을 위해 필요한 메모리의 양
- 얼마나 많은 메모리를 차지하는지

빅오표기법	내용
O(1)	상수 시간
O(logN)	로그 시간
O(N)	선형 시간
O(NlogN)	로그 선형 시간
O(N^2)	이차 시간
O(N^3)	삼차 시간
O(2^N)	지수 시간

O(1)이 가장 빠르고 밑으로 갈수록 느리다.

정렬

정렬 알고리즘은 시간 복잡도에 따라 성능이 달라진다.

[정렬 알고리즘 종류]

O(N^2) 시간 복잡도: 버블 정렬, 선택 정렬, 삽입 정렬
O(n log n) 시간 복잡도: 병합 정렬, 퀵 정렬

각각의 정렬 알고리즘을 살펴보자.

버블 정렬(= 단순 교환 정렬) : 이웃한 두 원소의 대소 관계를 비교해 필요하면 교환하며 반복됨

배열을 순회하면서 인접한 두 원소 비교
앞의 원소 > 뒤의 원소 : 위치를 바꿈
- arr[j], arr[j + 1] = arr[j + 1], arr[j]
순회를 돌고난 후면 가장 큰 원소가 맨 뒤로 이동함
최종적으로 정렬될 때까지 반복

  
def bubble_sort(arr):
  n = len(arr)
  for i in range(n - 1):
    swapped = False
    for j in range(n - i - 1):
      if arr[j] > arr[j + 1]:
        arr[j], arr[j + 1] = arr[j + 1], arr[j]
        swapped = True
    if not swapped:
      break

# 예제
data = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(data)
print(data) # [11, 12, 22, 25, 34, 64, 90]

선택 정렬

값이 작은 값을 찾고 난 후 맨 앞과 교환하면서 정렬될때까지 반복하기 때문에
앞에서부터 정렬이 되어나간다는 특징이 있다.

주어진 리스트에서 최솟값을 찾음
최솟값을 맨 앞의 요소와 교환
다음 인덱스로 이동 후, 최솟값을 찾고 교환
정렬될때까지 반복

  
def selection_sort(arr):
  n = len(arr)
  for i in range(n - 1):
    min_idx = i
    for j in range(i + 1, n):
      if arr[j] < arr[min_idx]:
        min_idx = j
    arr[i], arr[min_idx] = arr[min_idx], arr[i]

# 예제
data = [64, 25, 12, 22, 11]
selection_sort(data)
print(data) #[11, 12, 22, 25, 64]

삽입 정렬

주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입하며 정렬

두번째 요소부터 시작해 현재 요소를 삽입할 위치 찾음
현재 요소보다 큰 값들은 오른쪽으로 한 칸씩 이동
적절한 위치를 찾으면 현재 요소 삽입
정렬될때까지 반복

  
def insertion_sort(arr):
  for i in range(1, len(arr)):
    key = arr[i]
    j = i - 1
    while j >= 0 and arr[j] > key:
      arr[j + 1] = arr[j]
      j -= 1
    arr[j + 1] = key

# 예제
data = [8, 4, 6, 2, 9, 1, 3, 7, 5]
insertion_sort(data)
print(data) #[1,2,3,4,5,6,7,8,9]

여기까지 최악의 시간복잡도가 O(N^2)인 정렬 알고리즘이었다.
이제 O(n log n)의 시간 복잡도를 가지고 있는 정렬 알고리즘들에 대해 알아보자.

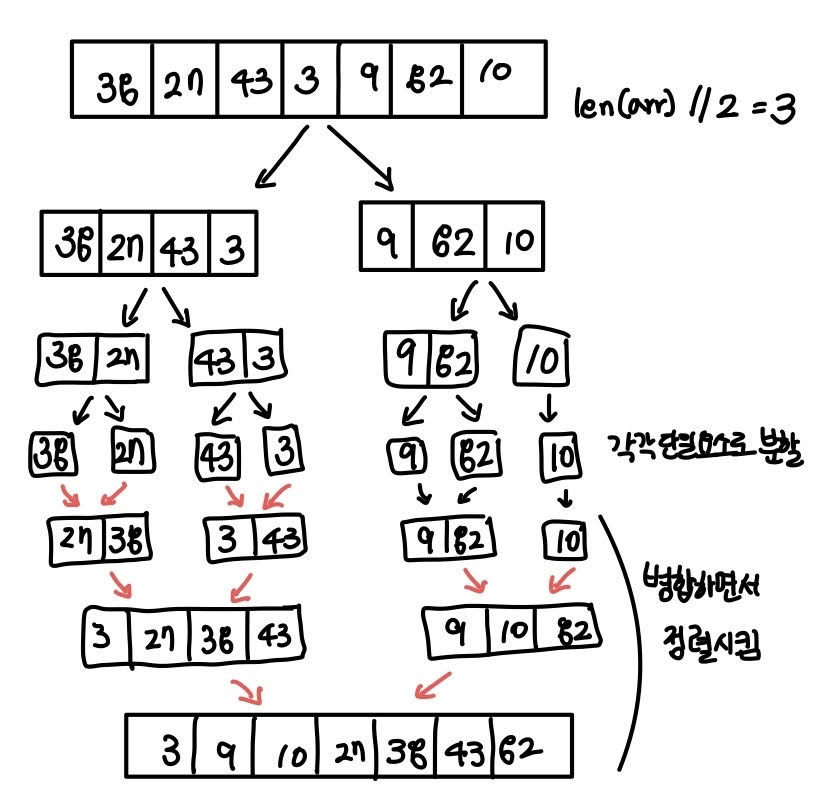
병합 정렬 (Merge Sort)

배열을 앞부분, 뒷부분으로 나눠 각각 정렬 후 병합하여 정렬

리스트의 길이가 1이 될때까지 분할
부분 리스트를 병합함

  
def merge_sort(arr):
  if len(arr) < 2:
    return arr

  mid = len(arr) // 2
  left = merge_sort(arr[:mid])
  right = merge_sort(arr[mid:])

  return merge(left, right)

def merge(left, right):
  sorted_arr = []
  i = j = 0

  while i < len(left) and j < len(right):
    if left[i] < right[j]:
      sorted_arr.append(left[i])
      i += 1
    else:
      sorted_arr.append(right[j])
      j += 1

    sorted_arr.extend(left[i:])
    sorted_arr.extend(right[j:])
    return sorted_arr

# 예제
data = [38, 27, 43, 3, 9, 82, 10]
sorted_data = merge_sort(data)
print(sorted_data) #[3, 9, 10, 27, 38, 43, 82]

퀵 정렬 (Quick Sort)

기준 데이터(pivot)를 설정 후 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸며 정렬

피벗(pivot)을 선택
피벗보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 분할
분할된 왼쪽, 오른쪽 배열에 대해 다시 퀵 정렬

  
def quick_sort(arr):
  if len(arr) <= 1:
    return arr

  pivot_index = len(arr) // 2
  pivot = arr[pivot_index]
  front_arr, pivot_arr, back_arr = [], [], []

  for value in arr:
    if value < pivot:
      front_arr.append(value)
    elif value > pivot:
      back_arr.append(value)
    else:
      pivot_arr.append(value)

  return quick_sort(front_arr) + pivot_arr + quick_sort(back_arr)

# 예제
arr = [9,11,20,30,3,4,1,50]
sorted_arr = quick_sort(arr)
print(sorted_arr) # [1, 3, 4, 9, 11, 20, 30, 50]

퀵 정렬은 피벗(pivot)을 잘 선택해야한다.
피벗을 최악으로 선택할 경우 엄청 느려지기 때문이다.
또한 퀵 정렬은 불안정적인 정렬이며, 같은 값일때 순서가 변경될 수 있다는 문제점이 있다.

퀵 정렬과 병합 정렬의 차이점

	퀵 정렬	병합 정렬
데이터 크기	데이터 크기가 클수록 효율적	데이터 크기와 상관 없이 일정한 성능
데이터가 정렬된 경우	최악의 경우 발생 (랜덤 피벗 선택 필요)	일정한 성능 유지
안정성	비안정 정렬	안정 정렬

Q. 퀵 정렬은 안전하지 않은 정렬인데, 많이 사용하는 이유?
평균적으로 퀵 정렬은 매우 빠르게 정렬이 되며, 적은 메모리를 사용합니다. 그리고 퀵 정렬은 캐시 효율성이 좋아서 실제 환경에서 성능이 좋습니다.

Q. 그럼 캐시 효율성이 왜 좋은걸까?
퀵 정렬은 제자리 정렬 방식으로 동작하여 배열 내에서 원소들의 순서를 변경하는 방식으로 정렬을 수행합니다. 이 과정에서 추가적인 메모리 공간을 거의 사용하지 않기 때문에 캐시 효율성을 높일 수 있습니다. 또한 퀵 정렬은 배열을 분할하는 방식에서 CPU 캐시와 잘 맞물려 작동하는데, 이는 배열의 인접한 데이터들을 차례로 처리하게 되어 CPU 캐시의 효율적 활용을 가능하게 만듭니다. 따라서 퀵 정렬은 비안정 정렬(정렬된 순서가 같아도 입력 순서가 보장되지 않는다)이지만 실제 환경에서는 뛰어난 성능을 보여주기 때문에 많이 사용됩니다.

KraftonJungle, keyword

jungle