[3주차 공부 키워드] 이진 트리와 최소 신장 트리

Posted Apr 1, 2025

By sihyun 18 min read

글의 목차

이번 글에선 이진 트리와 최소 신장 트리에 관한 내용을 다룹니다

트리
이진 트리 (Binary Tree)
이진 트리 순회 (전위, 중위, 후위 순회)
최소 신장 트리 (Minimum Spanning Tree)
4-1. 찾는데 사용되는 알고리즘 2가지 (크루스칼, 프림)

트리

트리는 그래프와 같이 노드(Node) 와 노드간을 연결하는 간선(Edge) 으로 구성된 자료구조
두 개의 노드 사이에 반드시 1개의 경로만을 가진다
또한 부모-자식 관계가 성립하기에 계층형 모델이라고도 한다

부모-자식 관계가 존재하여 레벨이 존재함 (Root : 최상위 노드)
노드가 N개이면 간선은 N -1개, 각 레벨 k에 존재하는 노드는 2^k개(완전이진트리)
방향성이 존재하고 사이클은 존재하지 않음

용어	의미
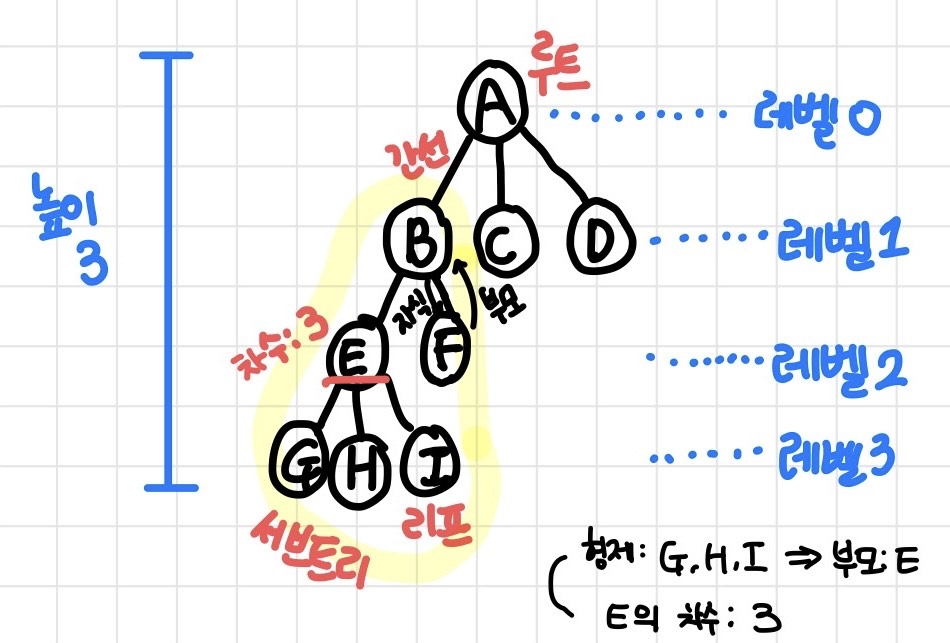
루트	가장 위쪽에 있는 노드 (트리 하나 당 1개만 존재)
리프 (leaf)	가장 아래쪽에 있는 노드 (자식이 없는 노드)
형제	부모가 같은 노드
레벨	루트에서 얼마나 멀리 떨어져있는지
차수	각 노드가 갖는 자식의 수
높이	루트에서 가장 멀리 있는 리프까지의 거리
서브트리	어떤 노드를 루트로 하고 그 자손으로 구성된 트리

그래프와 트리의 차이

	그래프	트리
방향성	방향, 무방향	방향만 존재
사이클	순환, 비순환, 자기순환	비순환
루트노드	루트 개념 X	한개의 루트 존재
부모, 자식	부모,자식 개념 X	1개의 부모노드 (루트 제외함)
간선 수	자유	N-1개
순회 유형	DFS,BFS 알고리즘	전위,중위,후위 순회
모델	네트워크 모델	계층 모델

이진 트리 (Binary Tree)

각 노드의 자식 노드가 최대 2개인 트리
이진트리의 깊이 h에 최대 2^(h-1)만큼 노드를 가질 수 있다

  
# 노드 클래스
class Node:
  def __init__(self, data):
    self.data = data
    self.left = None
    self.right = None

# 이진 트리
class BinaryTree():
  def __init__(self, root_data):
    self.root = Node(root_data)

이진 트리 종류

정 이진 트리 (Full binary tree) : 각 노드의 차수가 0 혹은 2인 이진 트리
- 자식이 없는 노드들은 모두 리프 노드, 나머지 노드들은 반드시 자식노드 수가 2개
포화 이진 트리 (Perfect binary tree) : 모든 리프 노드의 레벨이 동일하며 모든 레벨이 가득 채워져 있음
완전 이진 트리 (Complete binary tree) : 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하며, 마지막 레벨 노드는 전부 차 있지 않아도 되지만 왼쪽은 채워져야함
편향 트리(=사향트리) (Skewed Binary Tree) : 한쪽 방향으로만 자식 노드가 있음
균형 이진 트리(Balanced Binary Tree) : 트리의 모든 서브트리들이 균형을 이룸
- ex. AVL 트리, Red-Black 트리

이진 트리 순회 (전위 순회, 중위순회, 후위순회)

트리의 모든 노드를 방문하는 3가지 방식의 순회 알고리즘이 있다
노드 방문 순서에 따라 전위 순회, 중위 순회, 후위 순회로 구분된다

전위 순회 (Pre-order Traversal)

“부모 → 왼쪽 자식 → 오른쪽 자식” 순서로 탐색
즉 루트 → 왼쪽 서브 트리 → 오른쪽 서브 트리

현재 노드를 방문 (부모)
왼쪽 서브트리 순회
오른쪽 서브트리 순회

  
# 전위 순회
tree = [0, '1', '2', '3', '4', '5', '6', '7', '8']

def preorder(now):
  if now <= len(tree) -1:
    print(tree[now], end = ' ')
    preorder(now * 2)
    preorder(now * 2 + 1)

preorder(1)

1 2 4 8 5 3 6 7

중위 순회 (In-order Traversal)

“왼쪽 자식 → 부모 → 오른쪽 자식” 순서로 탐색
즉 왼쪽 서브 트리 → 루트 → 오른쪽 서브 트리

왼쪽 서브트리 순회
현재 노드 방문 (부모)
오른쪽 서브트리 순회

  
# 중위 순회
tree = [0, '1', '2', '3', '4', '5', '6', '7', '8']

def inorder(now):
  if now <= len(tree) -1:
    inorder(now * 2)
    print(tree[now], end = ' ')
    inorder(now * 2 + 1)

inorder(1)

8 4 2 5 1 6 3 7

후위 순회 (Post-order Traversal)

“왼쪽 자식 → 오른쪽 자식 → 부모” 순서로 탐색
즉 왼쪽 서브 트리 → 오른쪽 서브 트리 → 루트

왼쪽 서브트리 순회
오른쪽 서브트리 순회
현재 노드 방문 (부모)

  
# 후위 순회
tree = [0, '1', '2', '3', '4', '5', '6', '7', '8']

def postorder(now):
  if now <= len(tree) -1:
    postorder(now * 2)
    postorder(now * 2 + 1)
    print(tree[now], end = ' ')

postorder(1)

8 4 5 2 6 7 3 1

이진 탐색 트리(Binary Search Tree)

이진 탐색 트리는 아래의 조건을 만족하는 이진 트리이다

노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다
노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다
왼쪽, 오른쪽 서브트리도 이진 탐색 트리다

이진 트리는 탐색값이 존재하는지 확인하려면 트리 전체를 탐색해야하지만,
이진 탐색 트리는 왼쪽은 작은 수, 오른쪽은 큰 수들로 분리되어있어 값의 존재여부를 탐색하는데에 있어 O(logN)시간 복잡도를 가진다.

최소 신장 트리 (Minimum Spanning Tree = MST)

신장 트리란?
모든 노드가 연결되지만 사이클이 존재하지 않는 부분 그래프
그래프의 최소 연결 부분 그래프라고 함
연결 그래프에서 신장 트리는 1개가 아닌 다수일 수 있음

가능한 신장 트리 중 가중치 합이 가장 작은 트리를 최소 신장 트리라고 한다
최소한의 (간선) 비용으로 그래프의 모든 노드를 연결하는 트리이다

최소 신장 트리의 특징

간선의 가중치 합이 최소여야 함
노드가 n개일때, 간선은 반드시 n-1개
사이클이 존재 X

최소 신장 트리를 찾는 데 사용되는 알고리즘에는 2가지가 있다
크루스칼(Kruskal), 프림(Prim) 알고리즘이다

1. 크루스칼 알고리즘

가장 적은 간선 비용으로 모든 노드를 연결 할 수 있도록 함

[동작 과정]

주어진 모든 간선 정보에 대해 간선 비용이 낮은 순서로 정렬 (오름차순)
정렬된 간선 정보를 하나씩 확인하며 현재의 간선이 노드들 간의 사이클을 발생시키는지 확인함
2-1. 사이클이 발생 X → 최소 신장 트리에 포함
2-2. 사이클 발생 O → 최소 신장 트리에 포함 X
모든 간선 정보에 대해 2번 과정을 반복 수행
3-1. N-1개의 간선이 추가될 때까지 반복함 (N : 노드의 수)

Q. 그렇다면 위 동작 과정 중에 ‘현재 간선이 노드들 간의 사이클을 발생시키는지 확인’은 어떻게 할까요?
서로소 집합(disjoint set)자료구조의 union, find 연산을 사용해 확인한다

union : 두개의 원소가 각각 포함되어 있는 집합을 하나의 그룹으로 합침
find : 특정한 원소가 속한 집합(그룹)을 찾아줌

Q. 이 두가지 연산을 어떻게 활용시키나요?
find연산으로는 트리의 루트노드를 찾고, 그 루트노드를 통해 특정 집합을 표현함
union연산으로 두 원소에 대해 find연산을 수행해 각각의 루트노드를 찾고, 한 쪽의 루트노드를 다른 쪽에 합침으로써 하나의 트리로 만듬

  
import sys
input = sys.stdin.readline

# 특정 원소가 속한 집합 찾기 (find) - 경로 압축 기법 적용
def find_parent(parent, x):
  if parent[x] != x:
    parent[x] = find_parent(parent, parent[x])
  return parent[x]

# 두 원소가 속한 집합을 하나의 그룹으로 합침 (union)
def union_parent(parent, a, b):
  a = find_parent(parent, a)
  b = find_parent(parent, b)
  if a < b:
    parent[b] = a
  else:
    parent[a] = b

# v : 노드 개수, e : 간선의 개수
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화

# 부모를 자기 자신으로 일단 초기화 시킴
for i in range(1, v + 1):
  parent[i] = i

cycle = False
for _ in range(e):
  a, b = map(int, input().split())
  if find_parent(parent, a) == find_parent(parent, b):
    cycle = True
    break
  else:
    union_parent(parent, a, b)

if cycle:
  print("사이클 존재")
else:
  print("사이클 존재하지 않음")

find_parent, union_parent 함수를 사용해 사이클 여부를 판단한다

Q. 경로 압축 기법이란?
find 연산을 수행 시, 방문한 노드들에 대해 노드들의 부모를 root로 갱신시킴
다음에 find 연산을 수행하면 경로를 압축한 노드들은 부모값이 이미 root로 갱신되었기에 root를 찾는 비용을 아낄 수 있다

  
# 최종 루트노드를 조회하기위해 또 재귀적으로 호출해야하므로 시간복잡도 증가
def find_parent(parent, x):
  if parent[x] != x:
    return find_parent(parent, parent[x])
  return x

# 경로 압축 기법 (미리 부모 테이블에 부모 노드 값 갱신시켜둠)
def find_parent(parent, x):
  if parent[x] != x:
    parent[x] = find_parent(parent, parent[x])
  return parent[x]

[최소 신장 트리의 가중치 합 구하는 최종 코드]

  
import sys
input = sys.stdin.readline

# 특정 원소가 속한 집합 찾기 (find) - 경로 압축 기법 적용
def find_parent(parent, x):
  if parent[x] != x:
    parent[x] = find_parent(parent, parent[x])
  return parent[x]

# 두 원소가 속한 집합을 하나의 그룹으로 합침 (union)
def union_parent(parent, a, b):
  a = find_parent(parent, a)
  b = find_parent(parent, b)
  if a < b:
    parent[b] = a
  else:
    parent[a] = b

# v : 노드 개수, e : 간선의 개수
v, e = map(int, input().split())
parent = [0] * (v + 1)
for i in range(1, v + 1):
  parent[i] = i

edges = []
total_cost = 0

for _ in range(e):
  a, b, cost = map(int, input().split())
  edges.append((cost, a, b))

# 간선 정보 비용 기준으로 오름차순 정렬
edges.sort(key = lambda x : x[0])

for i in range(e):
  cost, a, b = edges[i]
  if find_parent(parent, a) != find_parent(parent, b):
    union_parent(parent, a, b)
    total_cost += cost

print(total_cost)

2. 프림 알고리즘

프림 알고리즘은 무방향 그래프에서 동작한다
한쪽 방향만 저장하게 되면 방문한 노드에서 연결된 간선을 찾지 못하기 때문이다

간단하게 실생활 속 예시를 들어보면 도시 내 대중교통 노선 설계를 생각해보자.
ex. 최소 비용으로 지하철 노선을 설계

한 역에서 시작 → 가장 적은 비용으로 연결할 수 있는 역을 추가 → 노선 확장
이 과정에서 어느 방향에서 접근하든 간선의 가중치(건설 비용)는 동일해야함 → 즉 양방향 그래프여야함

즉 프림 알고리즘은 모든 노드를 연결하며 최소 비용을 찾아야하므로 무방향 그래프여야한다